Quicksort algorithm is one of the most used sorting algorithms, especially to sort the large lists, and most of the programming languages, libraries have implemented it in one or another way. In Java, Arrays.sort() method sorts primitive data types using a double-pivot Quicksort algorithm, authored by Joshua Bloch and others. This implementation provides better performance for a lot of data sets, where traditional quicksort algorithms reduced into quadratic performance. This method also uses MergeSort, another good sorting algorithm, to sort objects. Quicksort implementations are also available in the C++ STL library.
Have you ever thought why quicksort is so popular? because on average it is one of the fastest sorting algorithms we have. On average quicksort is an O(n log n) algorithm, while it's the worst case is O(n^2), which is much better comparing with Bubble Sort or Insertion Sort.
It's also one of the popular algorithm interview questions, so as a programmer you must know how Quicksort works as well as how to implement Quicksort in Java or any other programming language.
One of the most important thing interviewer look in your quicksort implementation is the choice of the pivot and whether you are sorting in place or not. In "in-place" sorting, actual sorting takes place in the same array and no additional space is needed.
Due to this reason, quicksort is very efficient in sorting a large list of numbers, as no additional memory is required, a very space-efficient sorting algorithm. Quicksort is also one of the naturally recursive algorithms and serves a good exercise for Java programmers to master the art of recursion.
Also, basic knowledge of essential data structure is also very important and that's why I suggest all Java programmers join a comprehensive Data Structure and Algorithms course like Data Structures and Algorithms: Deep Dive Using Java on Udemy to fill the gaps in your understanding.
Steps to implement Quick sort algorithm in place:
1. Choose an element, called pivot, from the list or array. Generally pivot is the middle element of array.
2. Reorder the list so that all elements with values less than the pivot come before the pivot, and all elements with values greater than the pivot come after it (equal values can go either way). This is also known as partitioning. After partitioning the pivot is in its final position.
3. Recursively apply the above steps to the sub-list of elements with smaller values and separately the sub-list of elements with greater values. If the array contains only one element or zero elements then the array is sorted.
Following GIF image will help you to understand the working of the Quicksort algorithm a little better. In this image we have an array of integers which is not sorted and we need to sort them in ascending order. Our array is {6, 5, 3, 1, 8, 7, 2, 4} and we first choose 3 as pivot.
Have you ever thought why quicksort is so popular? because on average it is one of the fastest sorting algorithms we have. On average quicksort is an O(n log n) algorithm, while it's the worst case is O(n^2), which is much better comparing with Bubble Sort or Insertion Sort.
It's also one of the popular algorithm interview questions, so as a programmer you must know how Quicksort works as well as how to implement Quicksort in Java or any other programming language.
One of the most important thing interviewer look in your quicksort implementation is the choice of the pivot and whether you are sorting in place or not. In "in-place" sorting, actual sorting takes place in the same array and no additional space is needed.
Due to this reason, quicksort is very efficient in sorting a large list of numbers, as no additional memory is required, a very space-efficient sorting algorithm. Quicksort is also one of the naturally recursive algorithms and serves a good exercise for Java programmers to master the art of recursion.
Also, basic knowledge of essential data structure is also very important and that's why I suggest all Java programmers join a comprehensive Data Structure and Algorithms course like Data Structures and Algorithms: Deep Dive Using Java on Udemy to fill the gaps in your understanding.
How Quicksort Algorithm works? Example
Quicksort is a divide and conquer algorithm, which means the original list is divided into multiple lists, each of them is sorted individually, and then sorted output is merged to produce the sorted list. Here is a step by step explanation of how quicksort algorithm works.Steps to implement Quick sort algorithm in place:
1. Choose an element, called pivot, from the list or array. Generally pivot is the middle element of array.
2. Reorder the list so that all elements with values less than the pivot come before the pivot, and all elements with values greater than the pivot come after it (equal values can go either way). This is also known as partitioning. After partitioning the pivot is in its final position.
3. Recursively apply the above steps to the sub-list of elements with smaller values and separately the sub-list of elements with greater values. If the array contains only one element or zero elements then the array is sorted.
Following GIF image will help you to understand the working of the Quicksort algorithm a little better. In this image we have an array of integers which is not sorted and we need to sort them in ascending order. Our array is {6, 5, 3, 1, 8, 7, 2, 4} and we first choose 3 as pivot.
Now partitioning starts and we pick 6 on left side of side, because its greater than 3. Now on right side, we leave 4 because its greater than 3, and pick 2 for swapping with 6. After swapping our list look like {2, 5, 3, 1, 8, 7, 6, 4}.
Now we pick 5 on left side, and 1 on right side because it's greater than 3 and swap them again. Now, our array looks like {2, 1, 3, 5, 8, 7, 6, 4}. Since we are done with all elements with respect to 3 as pivot, we can now take the sub-array at left side of 3 and apply the same procedure.
This will sort the left array. Now on right side, we choose 4 as pivot, and repeat same procedure, which result in 4 swapped against 5. Now we take right side again with 6 as pivot and apply same procedure.
Now we pick 5 on left side, and 1 on right side because it's greater than 3 and swap them again. Now, our array looks like {2, 1, 3, 5, 8, 7, 6, 4}. Since we are done with all elements with respect to 3 as pivot, we can now take the sub-array at left side of 3 and apply the same procedure.
This will sort the left array. Now on right side, we choose 4 as pivot, and repeat same procedure, which result in 4 swapped against 5. Now we take right side again with 6 as pivot and apply same procedure.
Sorting an array of integer using QuickSort sorting algorithm
Java Program to implement the Quicksort Algorithm
Here is a Java program to sort an array of integers using the QuickSort algorithm. It is an in-place, recursive implementation of QuickSort. Logic is encapsulated in QuickSort class, and method quickSort(int low, int high).This method is called recursively to sort the array. This algorithm work exactly as explained in above GIF image, so if you understand the logic there, its very easy to write by your own.
1. QuickSort is a divide and conquer algorithm. Large list is divided into two and sorted separately (conquered), sorted list is merge later.
2. On "in-place" implementation of quick sort, list is sorted using same array, no additional array is required. Numbers are rearranged pivot, also known as partitioning.
3. Partitioning happen around pivot, which is usually middle element of array.
4. Average case time complexity of Quicksort is O(n log n) and worst case time complexity is O(n ^2), which makes it one of the fastest sorting algorithm. Interesting thing is it's worst case performance is equal to Bubble Sort :)
5. Quicksort can be implemented with an in-place partitioning algorithm, so the entire sort can be done with only O(log n) additional space used by the stack during the recursion.
6. Quicksort is also a good example of algorithm which makes best use of CPU caches, because of it's divide and conquer nature.
7. In Java, Arrays.sort() method uses quicksort algorithm to sort array of primitives. It's different than our algorithm, and uses two pivots. An important thing is that it perform much better than most of the quicksort algorithm available on internet for different data sets, where traditional quick sort perform poorly. One more reason, not to reinvent the wheel but to use the library method, when it comes to write production code.
That's all about Quicksort sorting algorithm in Java. It is one of the must know algorithm for all level of Java programmers, not that you need it often to implement it but to do well on interviews and use the lesson learned while implementing quicksort in Java. In our example, we have implemented quicksort "in-place", which is what you should do if asked to write quicksort in Java.
Remember as Java programmer, you don't need to write your own implementation as library implementation is much better implemented and tested. You should use Arrays.sort() method to sort your array instead of writing your own sort method.
One more reason for using library method is that they are usually improved over different version, and can take advantage of new machine instructions or native improvement.
Other Data Structure and Algorithms Articles and tutorials for you
import java.util.Arrays; /** * Test class to sort array of integers using Quicksort algorithm in Java. * @author Javin Paul */ public class QuickSortDemo{ public static void main(String args[]) { // unsorted integer array int[] unsorted = {6, 5, 3, 1, 8, 7, 2, 4}; System.out.println("Unsorted array :" + Arrays.toString(unsorted)); QuickSort algorithm = new QuickSort(); // sorting integer array using quicksort algorithm algorithm.sort(unsorted); // printing sorted array System.out.println("Sorted array :" + Arrays.toString(unsorted)); } } /** * Java Program sort numbers using QuickSort Algorithm. QuickSort is a divide * and conquer algorithm, which divides the original list, sort it and then * merge it to create sorted output. * * @author Javin Paul */ class QuickSort { private int input[]; private int length; public void sort(int[] numbers) { if (numbers == null || numbers.length == 0) { return; } this.input = numbers; length = numbers.length; quickSort(0, length - 1); } /* * This method implements in-place quicksort algorithm recursively. */ private void quickSort(int low, int high) { int i = low; int j = high; // pivot is middle index int pivot = input[low + (high - low) / 2]; // Divide into two arrays while (i <= j) { /** * As shown in above image, In each iteration, we will identify a * number from left side which is greater then the pivot value, and * a number from right side which is less then the pivot value. Once * search is complete, we can swap both numbers. */ while (input[i] < pivot) { i++; } while (input[j] > pivot) { j--; } if (i <= j) { swap(i, j); // move index to next position on both sides i++; j--; } } // calls quickSort() method recursively if (low < j) { quickSort(low, j); } if (i < high) { quickSort(i, high); } } private void swap(int i, int j) { int temp = input[i]; input[i] = input[j]; input[j] = temp; } } Output : Unsorted array :[6, 5, 3, 1, 8, 7, 2, 4] Sorted array :[1, 2, 3, 4, 5, 6, 7, 8]
Import points about the Quicksort algorithm
Now we know how quick sort works and how to implement quicksort in Java, its time to revise some of the important points about this popular sorting algorithm.1. QuickSort is a divide and conquer algorithm. Large list is divided into two and sorted separately (conquered), sorted list is merge later.
2. On "in-place" implementation of quick sort, list is sorted using same array, no additional array is required. Numbers are rearranged pivot, also known as partitioning.
3. Partitioning happen around pivot, which is usually middle element of array.
4. Average case time complexity of Quicksort is O(n log n) and worst case time complexity is O(n ^2), which makes it one of the fastest sorting algorithm. Interesting thing is it's worst case performance is equal to Bubble Sort :)
5. Quicksort can be implemented with an in-place partitioning algorithm, so the entire sort can be done with only O(log n) additional space used by the stack during the recursion.
6. Quicksort is also a good example of algorithm which makes best use of CPU caches, because of it's divide and conquer nature.
7. In Java, Arrays.sort() method uses quicksort algorithm to sort array of primitives. It's different than our algorithm, and uses two pivots. An important thing is that it perform much better than most of the quicksort algorithm available on internet for different data sets, where traditional quick sort perform poorly. One more reason, not to reinvent the wheel but to use the library method, when it comes to write production code.
That's all about Quicksort sorting algorithm in Java. It is one of the must know algorithm for all level of Java programmers, not that you need it often to implement it but to do well on interviews and use the lesson learned while implementing quicksort in Java. In our example, we have implemented quicksort "in-place", which is what you should do if asked to write quicksort in Java.
Remember as Java programmer, you don't need to write your own implementation as library implementation is much better implemented and tested. You should use Arrays.sort() method to sort your array instead of writing your own sort method.
One more reason for using library method is that they are usually improved over different version, and can take advantage of new machine instructions or native improvement.
Other Data Structure and Algorithms Articles and tutorials for you
- How to check if String is Palindrome? (solution)
- Top 20 String based coding problems for Java programmers? [problems]
- Top 10 Programming and Coding exercises for Java programmers? [problems]
- Top 50 Java Programs from Coding Interviews (see here)
- Top 30 Array-based programming problems for Java programmers? [problems]
- 10 Algorithm books Every Programmer Should Read (list)
- 5 Books to learn data structure and algorithms in Java? (books)
- How to reverse String in Java using Iteration and Recursion? (solution)
- 100+ Data Structure Coding Problems from Interviews (questions)
- 10 Free Data Structure and Algorithm Courses for Programmers (courses)
- How to count the occurrence of a given character in String? (solution)
- How to find duplicate characters in Java String? [solution]
- How to find the square root of a number in Java? [solution]
- 5 Free Data Structure and Algorithms Courses for Programmers (courses)
- How to convert a numeric string to an int? (solution)
- How to reverse words in a sentence without using a library method? (solution)
- How to reverse a String in place in Java? (solution)
- How do find the top two numbers from the integer array? [solution]
- How to print the Fibonacci series in Java without using recursion? [solution]
- How to program to print the first non-repeated character from String? (solution)
And lastly, one question for you? Which one is your favorite sorting algorithm? Bubble sort, Insertion sort, Selection sort, quick sort, merge sort, heap sort, tim short, radix sort, counting sort or anything else?
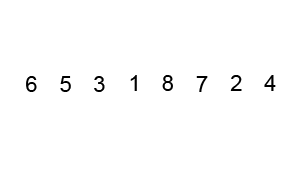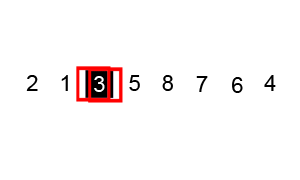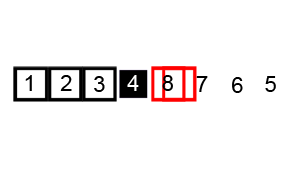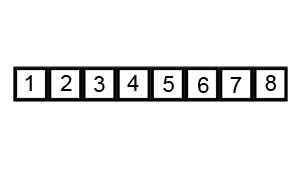
Hello Javin, nice article, I have been waiting for this ever since someone asked me following question :
ReplyDeleteExplain why recursive implementation of QuickSort will require O(log n) of additional space?
I have gone through the article, but not clear about how much additional space recursive implementation of quicksort is taking, could you please explain that in detail?
What is meaning of "double pivot" quick sort algorithm? Can you please elaborate how it perform better with classical Quicksort algo with just one pivot? an example would be great.
ReplyDeleteplease refer this link
ReplyDeletehttps://www.youtube.com/watch?v=3DV8GO9g7B4&list=PLEbnTDJUr_IeHYw_sfBOJ6gk5pie0yP-0&index=9&nohtml5=False
Hi Javin,
ReplyDeleteIt's nice:
if ( i <= j ) {
i++;
j--;
}
This makes slower the running time. Am I right?
public void quickSort(int[] arr, int p, int r){
ReplyDeleteif(p < r) {
int q = partition(arr, p, r);
quickSort(arr, p, q-1);
quickSort(arr, q+1, r);
}
}
public int partition(int arr[], int p, int r)
{
int i = p-1;
int pivot = arr[r];
for (int j = p; j <= r; j++) {
if(arr[j] <= pivot){
i++;
//do the swap
if(i!=j){
arr[i] = arr[i] ^ arr[j];
arr[j] = arr[i] ^ arr[j];
arr[i] = arr[i] ^ arr[j];
}
}
}
return i;
}
Does anyone tried to run the program.
ReplyDeleteIts not working.
@Unknown, what is the error your are getting?
ReplyDelete@Javin paul swapping condition to be (i < j) not the (i<=j) . getting wrong result if we sort 1 3 4 8 7 6 5 2
ReplyDeletetried with input 10, 30, 80, 90, 40, 50, 70 but it dint worked. even after sravan's change
ReplyDelete@sravan chitari the program is working
ReplyDeleteHello guys, one of my reader Tomasz has some interesting insight about in-place quicksort algorithms which he mailed to me. I am reposting here for everyones benefit:
ReplyDelete- if you would like to achieve O(log n) extra memory bound, you need to be more careful with the recursion: the simple trick is to use recursion only to the smaller
subinterval out of [low, j] and [i, high] and sort bigger interval on the same recursion level (use sth like tail recursion https://en.wikipedia.org/wiki/Tail_call).
Without that trick the algorithm could take O(n) extra memory.
- technically speaking any algorithm that use Omega(1) extra memory is not in-place. This kind of implementation of quick-sort use O(log n) extra memory (recursion stack clearly counts as extra memory). In practice there is no difference between O(1) and O(log n), but if you would like to be strict it is worth to mention the difference.
Once again thanks to Tomasz for his input.
swap(i, j);
ReplyDeleteHere the elements must be swapped right not the indexes? So it should be swap(a[i],a[j])
can you provide not-in-place quicksort approach. Hope it will be helpful for everyone to understand the difference
ReplyDeleteI'm solve it with pick the pivot at last element and this example solved with lomuto partitioning algorithm and then in this logic and start from leftmost element and keep track of the index of smaller elements as i
ReplyDeleteor equal value .
while traversing if we find smaller element we swap the current element with arr[i] , otherwise we ignore the current element.
As partition is done recursivly , and putting the pivot in actual position repeatedly putting its pivot in their position makes array sorts.
1-the key process of this example is partition ()
2-the target of partitions to place the pivot in its correct position in sorted array .
3-and put all smaller element to the left of the pivot.
4-and all greater elements to the right of pivot.
5-partition is done recursivly each side of the pivot.
6-after the pivot is placed in correct position.
7-and sorts the array.
class QuickSort {
//utility function to swap tow element .
static void swaps (int arr [] , int i, int j)
int temp = arr[i ] ;
arr [i] = arr[j] ;
arr[j] = temp;
}
//this function takes last //element as pivot correct position.
//in sorted array and places //all smaller element to left
//of pivot and all greater
//element to right of pivot.
static int partition (int arr[] , int low, int high ) {
//choosing the pivot.
int pivot = arr[high] ;
//index of smaller element and indicates
//the right position of pivot found so far.
int i = (low - 1);
for (int j = low; j < high - 1 ; j++) {
//if current element less than
// the pivot
if (arr[j] < pivot ) {
//increment index of smaller
// element
i++;
swaps (arr, i, j) ;
}
}
swaps (arr , low + 1, high ) ;
return (i +1) ;
}
//the main function that implement //quick sort.
//arr [] - - > array to be sorted.
//low - - > starting index.
//high --> ending index.
static void quickSort (int arr [], int low, int high) {
//pi is partitioning index, arr[p]
//is now right.
int pi = partition (arr, int low, int high) ;
if (low < high ) {
//separately sort element before partition
// and after partition.
quickSort (arr, low, pi - 1) ;
quickSort (int arr , pi + 1, high ) ;
}
}
// print the sorted array.
static void printArr(int [] arr) {
for (int i =0; i < arr. length ; i ++) {
System. out. print ( arr[i] + " " ) ;
}
}
//driver code
public static void main (String args []) {
int arr [] = {} ;
int N = arr. length ;
system.out.println("sorted Array is : ") ;
//call function
quickSort (arr, 0, N - 1) ;
printArr(arr) ;
}
}
for more details to understand visit : https://www.geeksforgeeks.org/quick-sort-algorithm/