How to implement Post Order Traversal of Binary Tree in Java - Recursion and Iteration Example

This is the third article on tree traversal. In the last couple of articles, I have shown you how to implement preorder and inorder traversal in Java, both recursively and iteratively and today, you will learn about the post-order traversal. Out of these three main tree traversal algorithms, the post-order traversal is most difficult to implement, especially the iterative version. In postorder traversal, you first visit left subtree, then right subtree and at last you print the value of root or not. So, the value of root is always printed at last in the post-order traversal.

As I told you before, all three preOrder, inOrder, and postOrder are depth-first algorithms so they go down in the binary tree first before visiting nodes of the same level. The implementation of the recursive algorithm is very simple, you just need to adjust the order of recursive call according to the algorithm and you are done, but the iterative algorithm requires some effort to get it right, which you will see in this article.

Unlike inorder traversal which prints the nodes of the binary search tree in sorted order, post order doesn't print values in sorted order but can be used to generate a postfix representation of a binary tree.

It's also particularly important while deleting nodes of binary tree e.g. if you don't use post-order traversal during deletion, then you lose the references you need for deleting the child trees. 

These were just a couple of usage of post-order tree traversal, you can see a good algorithm book like Introduction to Algorithms by Thomas H. Cormen or Data Structures and Algorithms: Deep Dive Using Java on Udemy to fill the gaps in your understanding.

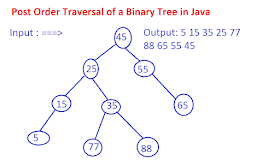
Problem statement:  Print nodes of the following binary tree in post order

        45
       / \
      25  55
     / \    \
    15  35   65
   /   /  \
  5   77   88

Output: 5 15 35 25 77 88 65 55 45 

Post Order traversal of binary tree in Java using Recursion

Let's first see the recursive solution which is extremely easy to code, especially if you know how to implement pre order and in order using recursion. All you need to do is change the order of recursive calls according to the algorithm as per the following steps of the post-order algorithm.

1) visit the left subtree
2) visit the right subtree
3) print the value of the current node or root.

So in the case of the given binary tree, we start with root(45) and then go to left, node(25), then again we go to left until we reach the leaf node 5. At this time, we try to go right subtree now, but there is nothing there so we print the value of the node. Now, we start to go up to node 15, there is no right subtree here so we again print the value of 15.

Now, we come back to 25, here we have the right subtree so we go there and reach another leaf node 35, we print its value and come back to 25 since both 15 and 35 are visited we print its value and go back to 45. Now we start to right subtree because the left subtree of node 45 is fully explored and reaches node 55. 

Since there is no left subtree, we go again to 65, which has left subtree, so we go to 77 and prints its value as its a leaf node, we come back to 65 and go to right subtree and print 88 because its leaf node, now we come back again to 65 and prints value.

Similarly, we go up to 55 and since the left and right subtree is fully explored we print its value and come back to the root. Now since both the left and right subtree of the root is fully visited, we print the value of root and algorithm finished since all nodes are visited.

Here is a post-order implementation in Java using recursion:

private void postOrder(TreeNode node) {
    if (node == null) {
      return;
    }

    postOrder(node.left);
    postOrder(node.right);
    System.out.printf("%s ", node.data);
  }

The code is exactly similar to recursive preOrder and InOrder algorithm with only change that postOrder() function call is now made for left and right subtree before printing value of the node.

The node == null is still serve ras base case of this solution. Btw, if you struggle with recursion or understand recursion but don't know how to come up with a recursive algorithm for a problem, I would suggest reading Grokking Algorithm, one of the newest books on the algorithm and I guess most readable of all of them.

Binary Tree Post Order Traversal in Java without Recursion

The iterative post order traversal algorithms are the most difficult between all three iterative tree traversal algorithms e.g. pre-order, in order, and post order. Like other iterative algorithms, we use a Stack to store nodes. We start with root by pushing it into Stack and loop until Stack is empty. In every iteration we peek() the current node from Stack, remember unlike preOrder, we use peek() and not pop() method.

The peek() method return the top of the Stack without removing it. If the current node is the lead node then we print its value. Otherwise, we check current node has a right and left subtree and then we push those nodes into Stack and mark them null to signify they are already in Stack or visited.

Since we need to visit the left subtree first, we push the right node first because Stack is a LIFO data structure and the last inserted node will remain at the top of the stack. we repeat the same process until we visit all the nodes, at this point tree is traversed using a post-order algorithm. 

If you want to learn more about Stack and how to convert a recursive algorithm to an iterative one, please refer to a good algorithm book like Introduction to Algorithms by Thomas H. Cormen.

Here is the Java implementation of iterative post-order traversal algorithm of a binary tree:

public void postOrderWithoutRecursion() {
    Stack nodes = new Stack<>();
    nodes.push(root);

    while (!nodes.isEmpty()) {
      TreeNode current = nodes.peek();

      if (current.isLeaf()) {
        TreeNode node = nodes.pop();
        System.out.printf("%s ", node.data);
      } else {

        if (current.right != null) {
          nodes.push(current.right);
          current.right = null;
        }

        if (current.left != null) {
          nodes.push(current.left);
          current.left = null;
        }
      }

    }
  }

You can see that we first check for leaf node and if it's leaf we print its value. Remember to mark current.left and current.right node null otherwise your program will never finish and the code will go into an infinite loop.

Java Program to traverse a binary tree in post order algorithm

Here is our complete program to print all nodes of a binary tree as per post-order traversal in Java. You can also use this algorithm to collect all nodes in a list, for now, we are just printing. This program implements post-order traversal both with and without recursion. 

We also use the same BinaryTree and TreeNode class that we have used to implement the binary search tree, the only difference is that this time we have not made TreeNode implements a Comparable interface. 

The recursive logic is coded in postOrder(TreeNode root) method and iterative algorithm is coded into postOrderWithoutRecursion() method.

import java.util.Stack;

/*
* Java Program to traverse a binary tree 
* using postOrder traversal without recursion. 
* In postOrder traversal first left subtree is visited, followed by
*  right subtree
* and finally data of root or current node is printed.
* 
* input:
*       45
*      / \
*     25  55
*    / \    \
*   15  35   65
*  /   /  \
* 5   77   88
* 
* output: 5 15 35 25 77 88 65 55 45 
*/

public class Main {

public static void main(String[] args) throws Exception {

// construct the binary tree given in question
BinaryTree bt = BinaryTree.create();

// traversing binary tree using post order traversal using recursion
System.out.println("printing nodes of binary tree on post order using 
                         recursion");

bt.postOrder();

System.out.println(); // insert new line

// traversing binary tree on post order traversal without recursion
System.out.println("printing nodes of binary tree on post order using 
                        iteration");
bt.postOrderWithoutRecursion();
}

}

class BinaryTree {
static class TreeNode {
String data;
TreeNode left, right;

TreeNode(String value) {
this.data = value;
left = right = null;
}

boolean isLeaf() {
return left == null ? right == null : false;
}

}

// root of binary tree
TreeNode root;

/**
* traverse the binary tree on post order traversal algorithm
*/
public void postOrder() {
postOrder(root);
}

private void postOrder(TreeNode node) {
if (node == null) {
return;
}

postOrder(node.left); 
postOrder(node.right);
System.out.printf("%s ", node.data);
}

public void postOrderWithoutRecursion() {
Stack nodes = new Stack<>();
nodes.push(root);

while (!nodes.isEmpty()) {
TreeNode current = nodes.peek();

if (current.isLeaf()) {
TreeNode node = nodes.pop();
System.out.printf("%s ", node.data);
} else {

if(current.right != null){
nodes.push(current.right);
current.right = null;
}

if(current.left != null){
nodes.push(current.left);
current.left = null;
}
}

}
}

/**
* Java method to create binary tree with test data
* 
* @return a sample binary tree for testing
*/
public static BinaryTree create() {
BinaryTree tree = new BinaryTree();
TreeNode root = new TreeNode("45");
tree.root = root;
tree.root.left = new TreeNode("25");
tree.root.left.left = new TreeNode("15");
tree.root.left.left.left = new TreeNode("5");

tree.root.left.right = new TreeNode("35");
tree.root.right = new TreeNode("55");
tree.root.right.right = new TreeNode("65");
tree.root.right.right.left = new TreeNode("77");
tree.root.right.right.right = new TreeNode("88");



return tree;
}

}

Output
printing nodes of a binary tree on post order using recursion
5 15 35 25 77 88 65 55 45 
printing nodes of a binary tree on post order using iteration
5 15 35 25 77 88 65 55 45 

That's all about how to traverse a binary tree in post order. The recursive post-order traversal is pretty easy but the iterative post-order algorithm is quite tough. This also shows the point that sometimes a recursive solution is much easier and readable than an iterative one e.g. posts order tree traversal or tower of Hanoi. 

The algorithm is simple but it's difficult to implement using Stack and candidates often make mistakes while coming up to the tree from the leaf node.

Nevertheless, this completes the three-part series of articles about binary tree traversal. I am thinking to extend this series to cover other tree traversal algorithms e.g. level order traversal or spiral level order traversal. 

In the meantime, if you want to enjoy learning algorithms, you can refer to these free data structure and algorithms courses, one of the best free resources for programmers with lots of real-world examples and a different style of explanation.

 Other binary tree and data structure tutorials you may like to explore

• 5 data structure and algorithm books for coding interviews (list)
• How to implement pre-order traversal in Java?  (solution)
• How to implement in-order traversal in Java? (solution)
• How to print all leaf nodes of a binary tree in Java? (solution)
• How to implement in-order traversal in Java without recursion? (solution)
• How to traverse a binary tree in pre-order without using recursion? (solution)
• How to print all leaf nodes of a binary tree without recursion in Java? (solution)
• How to implement linked lists using generic in Java? (solution)
• How to find the middle element of a linked list using a single pass? (solution)
• How to reverse a singly linked list in Java? (solution)
• How to find the 3rd element from the end of the linked list in Java? (solution)
• How to reverse an array in place in Java? (solution)
• How to print duplicate elements of an array in Java? (solution)